INTRODUCTORY THEORY OF CHROMATOGRAPHY
Introduction
Few methods of chemical analysis are truly specific to a particular analyte. It is often found that the analyte of interest must be separated from the myriad of individual compounds that may be present in a sample. As well as providing the analytical scientist with methods of separation, chromatographic techniques can also provide methods of analysis.
Chromatography involves a sample (or sample extract) being dissolved in a mobile phase (which may be a gas, a liquid or a supercritical fluid). The mobile phase is then forced through an immobile, immiscible stationary phase. The phases are chosen such that components of the sample have differing solubilities in each phase. A component which is quite soluble in the stationary phase will take longer to travel through it than a component which is not very soluble in the stationary phase but very soluble in the mobile phase. As a result of these differences in mobilities, sample components will become separated from each other as they travel through the stationary phase.
Techniques such as H.P.L.C. (High Performance Liquid Chromatography) and G.C. (Gas Chromatography) use columns - narrow tubes packed with stationary phase, through which the mobile phase is forced. The sample is transported through the column by continuous addition of mobile phase. This process is called elution. The average rate at which an analyte moves through the column is determined by the time it spends in the mobile phase.
Distribution of analytes between phases
The distribution of analytes between phases can often be described quite simply. An analyte is in equilibrium between the two phases;
Amobile <===> Astationary
The equilibrium constant, K, is termed the partition coefficient; defined as the molar concentration of analyte in the stationary phase divided by the molar concentration of the analyte in the mobile phase.
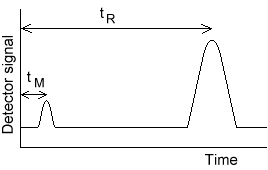
The time between sample injection and an analyte peak reaching a detector at the end of the column is termed the retention time (tR ). Each analyte in a sample will have a different retention time. The time taken for the mobile phase to pass through the column is called tM.
A term called the retention factor, k', is often used to describe the migration rate of an analyte on a column. You may also find it called the capacity factor. The retention factor for analyte A is defined as;
k'A = t R - tM / tM
t R and tM are easily obtained from a chromatogram. When an analytes retention factor is less than one, elution is so fast that accurate determination of the retention time is very difficult. High retention factors (greater than 20) mean that elution takes a very long time. Ideally, the retention factor for an analyte is between one and five.
We define a quantity called the selectivity factor, a , which describes the separation of two species (A and B) on the column;
a = k 'B / k 'A
When calculating the selectivity factor, species A elutes faster than species B. The selectivity factor is always greater than one.
Band broadening and column efficiency
To obtain optimal separations, sharp, symmetrical chromatographic peaks must be obtained. This means that band broadening must be limited. It is also beneficial to measure the efficiency of the column.
The Theoretical Plate Model of Chromatography
The plate model supposes that the chromatographic column is contains a large number of separate layers, called theoretical plates. Separate equilibrations of the sample between the stationary and mobile phase occur in these "plates". The analyte moves down the column by transfer of equilibrated mobile phase from one plate to the next.

It is important to remember that the plates do not really exist; they are a figment of the imagination that helps us understand the processes at work in the column.They also serve as a way of measuring column efficiency, either by stating the number of theoretical plates in a column, N (the more plates the better), or by stating the plate height; the Height Equivalent to a Theoretical Plate (the smaller the better).
If the length of the column is L, then the HETP is
HETP = L / N
The number of theoretical plates that a real column possesses can be found by examining a chromatographic peak after elution;
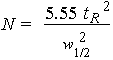
where w1/2 is the peak width at half-height.
As can be seen from this equation, columns behave as if they have different numbers of plates for different solutes in a mixture.
The Rate Theory of Chromatography
A more realistic description of the processes at work inside a column takes account of the time taken for the solute to equilibrate between the stationary and mobile phase (unlike the plate model, which assumes that equilibration is infinitely fast). The resulting band shape of a chromatographic peak is therefore affected by the rate of elution. It is also affected by the different paths available to solute molecules as they travel between particles of stationary phase. If we consider the various mechanisms which contribute to band broadening, we arrive at the Van Deemter equation for plate height;
HETP = A + B / u + C u
where u is the average velocity of the mobile phase. A, B, and C are factors which contribute to band broadening.
A - Eddy diffusion
The mobile phase moves through the column which is packed with stationary phase. Solute molecules will take different paths through the stationary phase at random. This will cause broadening of the solute band, because different paths are of different lengths.
B - Longitudinal diffusion
The concentration of analyte is less at the edges of the band than at the center. Analyte diffuses out from the center to the edges. This causes band broadening. If the velocity of the mobile phase is high then the analyte spends less time on the column, which decreases the effects of longitudinal diffusion.
C - Resistance to mass transfer
The analyte takes a certain amount of time to equilibrate between the stationary and mobile phase. If the velocity of the mobile phase is high, and the analyte has a strong affinity for the stationary phase, then the analyte in the mobile phase will move ahead of the analyte in the stationary phase. The band of analyte is broadened. The higher the velocity of mobile phase, the worse the broadening becomes.
Van Deemter plots
A plot of plate height vs. average linear velocity of mobile phase.
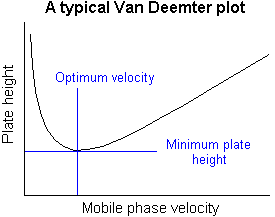
Such plots are of considerable use in determining the optimum mobile phase flow rate.
Resolution
Although the selectivity factor, a, describes the separation of band centres, it does not take into account peak widths. Another measure of how well species have been separated is provided by measurement of the resolution. The resolution of two species, A and B, is defined as
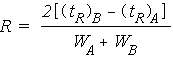
Baseline resolution is achieved when R = 1.5
It is useful to relate the resolution to the number of plates in the column, the selectivity factor and the retention factors of the two solutes;
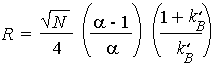
To obtain high resolution, the three terms must be maximised. An increase in N, the number of theoretical plates, by lengthening the column leads to an increase in retention time and increased band broadening - which may not be desirable. Instead, to increase the number of plates, the height equivalent to a theoretical plate can be reduced by reducing the size of the stationary phase particles.
It is often found that by controlling the capacity factor, k', separations can be greatly improved. This can be achieved by changing the temperature (in Gas Chromatography) or the composition of the mobile phase (in Liquid Chromatography).
The selectivity factor, a, can also be manipulated to improve separations. When a is close to unity, optimising k' and increasing N is not sufficient to give good separation in a reasonable time. In these cases, k' is optimised first, and then a is increased by one of the following procedures:
Changing mobile phase composition
Changing column temperature
Changing composition of stationary phase
Using special chemical effects (such as incorporating a species which complexes with one of the solutes into the stationary phase)
Few methods of chemical analysis are truly specific to a particular analyte. It is often found that the analyte of interest must be separated from the myriad of individual compounds that may be present in a sample. As well as providing the analytical scientist with methods of separation, chromatographic techniques can also provide methods of analysis.
Chromatography involves a sample (or sample extract) being dissolved in a mobile phase (which may be a gas, a liquid or a supercritical fluid). The mobile phase is then forced through an immobile, immiscible stationary phase. The phases are chosen such that components of the sample have differing solubilities in each phase. A component which is quite soluble in the stationary phase will take longer to travel through it than a component which is not very soluble in the stationary phase but very soluble in the mobile phase. As a result of these differences in mobilities, sample components will become separated from each other as they travel through the stationary phase.
Techniques such as H.P.L.C. (High Performance Liquid Chromatography) and G.C. (Gas Chromatography) use columns - narrow tubes packed with stationary phase, through which the mobile phase is forced. The sample is transported through the column by continuous addition of mobile phase. This process is called elution. The average rate at which an analyte moves through the column is determined by the time it spends in the mobile phase.
Distribution of analytes between phases
The distribution of analytes between phases can often be described quite simply. An analyte is in equilibrium between the two phases;
Amobile <===> Astationary
The equilibrium constant, K, is termed the partition coefficient; defined as the molar concentration of analyte in the stationary phase divided by the molar concentration of the analyte in the mobile phase.
The time between sample injection and an analyte peak reaching a detector at the end of the column is termed the retention time (tR ). Each analyte in a sample will have a different retention time. The time taken for the mobile phase to pass through the column is called tM.

A term called the retention factor, k', is often used to describe the migration rate of an analyte on a column. You may also find it called the capacity factor. The retention factor for analyte A is defined as;
k'A = t R - tM / tM
t R and tM are easily obtained from a chromatogram. When an analytes retention factor is less than one, elution is so fast that accurate determination of the retention time is very difficult. High retention factors (greater than 20) mean that elution takes a very long time. Ideally, the retention factor for an analyte is between one and five.
We define a quantity called the selectivity factor, a , which describes the separation of two species (A and B) on the column;
a = k 'B / k 'A
When calculating the selectivity factor, species A elutes faster than species B. The selectivity factor is always greater than one.
Band broadening and column efficiency
To obtain optimal separations, sharp, symmetrical chromatographic peaks must be obtained. This means that band broadening must be limited. It is also beneficial to measure the efficiency of the column.
The Theoretical Plate Model of Chromatography
The plate model supposes that the chromatographic column is contains a large number of separate layers, called theoretical plates. Separate equilibrations of the sample between the stationary and mobile phase occur in these "plates". The analyte moves down the column by transfer of equilibrated mobile phase from one plate to the next.

It is important to remember that the plates do not really exist; they are a figment of the imagination that helps us understand the processes at work in the column.They also serve as a way of measuring column efficiency, either by stating the number of theoretical plates in a column, N (the more plates the better), or by stating the plate height; the Height Equivalent to a Theoretical Plate (the smaller the better).
If the length of the column is L, then the HETP is
HETP = L / N
The number of theoretical plates that a real column possesses can be found by examining a chromatographic peak after elution;
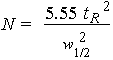
where w1/2 is the peak width at half-height.
As can be seen from this equation, columns behave as if they have different numbers of plates for different solutes in a mixture.
The Rate Theory of Chromatography
A more realistic description of the processes at work inside a column takes account of the time taken for the solute to equilibrate between the stationary and mobile phase (unlike the plate model, which assumes that equilibration is infinitely fast). The resulting band shape of a chromatographic peak is therefore affected by the rate of elution. It is also affected by the different paths available to solute molecules as they travel between particles of stationary phase. If we consider the various mechanisms which contribute to band broadening, we arrive at the Van Deemter equation for plate height;
HETP = A + B / u + C u
where u is the average velocity of the mobile phase. A, B, and C are factors which contribute to band broadening.
A - Eddy diffusion
The mobile phase moves through the column which is packed with stationary phase. Solute molecules will take different paths through the stationary phase at random. This will cause broadening of the solute band, because different paths are of different lengths.
B - Longitudinal diffusion
The concentration of analyte is less at the edges of the band than at the center. Analyte diffuses out from the center to the edges. This causes band broadening. If the velocity of the mobile phase is high then the analyte spends less time on the column, which decreases the effects of longitudinal diffusion.
C - Resistance to mass transfer
The analyte takes a certain amount of time to equilibrate between the stationary and mobile phase. If the velocity of the mobile phase is high, and the analyte has a strong affinity for the stationary phase, then the analyte in the mobile phase will move ahead of the analyte in the stationary phase. The band of analyte is broadened. The higher the velocity of mobile phase, the worse the broadening becomes.
Van Deemter plots
A plot of plate height vs. average linear velocity of mobile phase.

Such plots are of considerable use in determining the optimum mobile phase flow rate.
Resolution
Although the selectivity factor, a, describes the separation of band centres, it does not take into account peak widths. Another measure of how well species have been separated is provided by measurement of the resolution. The resolution of two species, A and B, is defined as
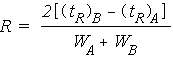
Baseline resolution is achieved when R = 1.5
It is useful to relate the resolution to the number of plates in the column, the selectivity factor and the retention factors of the two solutes;
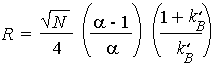
To obtain high resolution, the three terms must be maximised. An increase in N, the number of theoretical plates, by lengthening the column leads to an increase in retention time and increased band broadening - which may not be desirable. Instead, to increase the number of plates, the height equivalent to a theoretical plate can be reduced by reducing the size of the stationary phase particles.
It is often found that by controlling the capacity factor, k', separations can be greatly improved. This can be achieved by changing the temperature (in Gas Chromatography) or the composition of the mobile phase (in Liquid Chromatography).
The selectivity factor, a, can also be manipulated to improve separations. When a is close to unity, optimising k' and increasing N is not sufficient to give good separation in a reasonable time. In these cases, k' is optimised first, and then a is increased by one of the following procedures:
Changing mobile phase composition
Changing column temperature
Changing composition of stationary phase
Using special chemical effects (such as incorporating a species which complexes with one of the solutes into the stationary phase)

0 Comments:
Post a Comment
<< Home